拆分操作可用于建模形状并通过将较大的几何对象拆分为较小的对象来设置几何。拆分操作是使用 CGA 形状规则创建设计的核心。拆分的基本定义是:
拆分(轴){大小:操作}
有关详细信息,请参阅 CGA拆分操作。
以下示例显示了不同类型的拆分操作:
- 绝对分裂,
- 相对分裂,
- 浮动拆分和
- 重复拆分。
以下是从介绍性规则开始的示例,然后是每种拆分类型的示例。
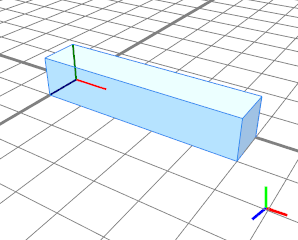
在这个介绍性规则中,我们调整初始范围的大小并在该范围内插入一个立方体。范围的 x 维度(立方体的长度)设置为 5。范围的 y 和 z 维度设置为 1。蓝色规则调整范围的 y 维度(立方体的高度)使用相对运算符 ‘相对于scope.sy 。因为规则参数height设置为1,所以立方体的高度保持不变。 |
 |
绝对分割
绝对分割以绝对值切割几何。
|
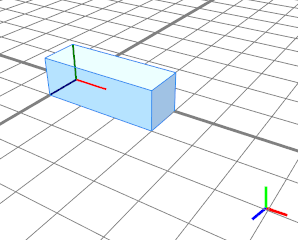
操作split(x) { 3 : Blue }沿范围的 x 维度拆分几何。长度为 5 的立方体以 3 个单位的绝对值切割,并替换为连续的立方体形状Blue。 |
 |
|
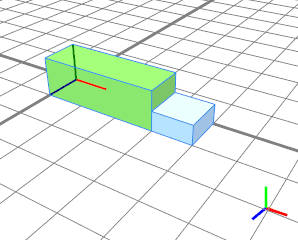
此示例显示如果使用两个绝对分割值(绿色 3 个单位和蓝色单位 1 个)会发生什么。拆分后的总长度为 3+1=4。 |
 |
|
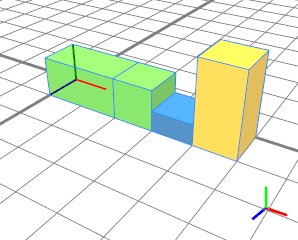
此示例显示了(有限)范围内绝对值的影响。生成的黄色形状的长度为 1 而不是 2,因为总长度为 5。不会生成最右边的蓝色形状。 |
 |
|
不会产生带有负值或零大小值的拆分。两个黄色形状都不会生成。蓝色从 1.5 开始。最后一个绿色形状在总长度为 5 处停止。 |
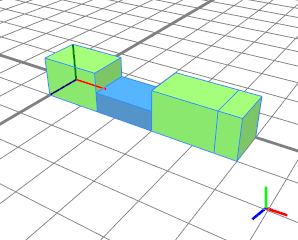 |
相对分割
相对拆分使用相对于范围大小而不是绝对值的比例。相对值由运算符‘后跟 0 到 1 之间的值表示。
|
此示例使用黄金分割率缩小范围。 |
 |
|
此示例显示了使用黄金分割率的递归拆分。当几何体变得太小而无法进一步拆分时,递归停止。 |
 |
浮动拆分
浮动拆分会调整值,以便填充整个空间。浮动拆分由运算符~表示。
|
在此示例中,拆分操作将长度为 5 的立方体拆分为 3 个单位(绿色)。然后以 1 个单位切割剩余的几何形状。这次使用浮动运算符~将 1 单位扩展到第一次切割的剩余空间,即 5-3=2 单位(蓝色)。 |
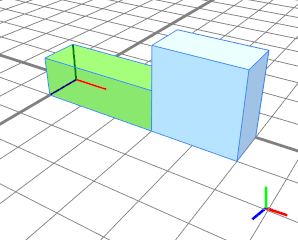 |
|
浮点值 2 填充两个绝对值(蓝色 1 个单位)之间的空间(黄色 3 个单位)。 |
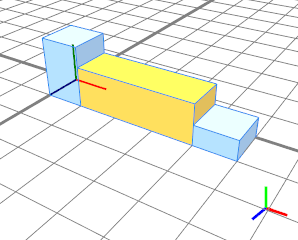 |
|
具有相同单位(每个 1.5)的多个浮动拆分均匀分布在剩余的作用域空间(2 个单位)上。 |
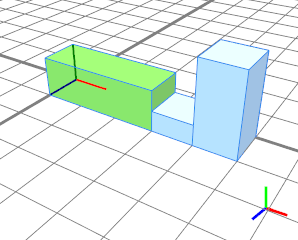 |
|
三个浮动分裂均匀分布。 |
 |
|
如果没有为浮动拆分留下空间,则不会生成相应的形状(在这种情况下为蓝色)。 |
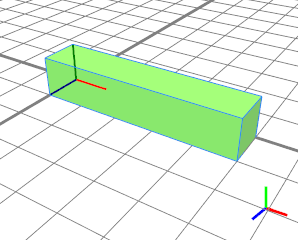 |
重复拆分
重复拆分用于在给定范围内重复几何图形。它创造了一种节奏:重复使用一组几何对象以建立可识别的模式。一个典型的场景是普通高层写字楼立面的窗户和柱子的交替布置。括号后的星号*表示重复拆分。
|
在第一个示例中,长度为 10 的范围用绝对长度为 2 的绿色形状重复填充。正好 5 个长度为 2 的立方体适合范围。 浮动值 2.1 会产生相同的结果,因为拆分为 5 个后续形状(每个长度为 2)仍然最接近 2.1 的目标长度。 |
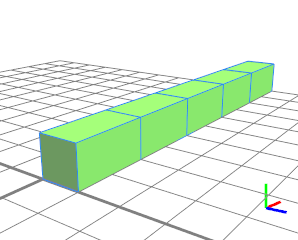 |
|
浮动重复拆分(绿色)以两个绝对拆分(蓝色)为边界。请注意,浮动分割的结果长度为 (10-2)/3≈2.66,这是目标值 2.5 的最佳近似值。 |
 |
|
重复绝对分割(绿色)将首先独立地在分割的哪一侧表示重复进行评估。浮动拆分不会生成任何空间。 |
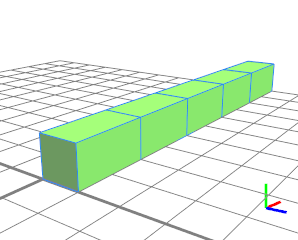 |
|
此示例显示具有绝对(或相对)值的重复拆分可以以两个相邻的浮动(或绝对)拆分为边界。 |
 |
|
第一次浮动拆分的大小和重复浮动拆分的大小相同。这 2 个单位平均分布 4 倍(蓝色)到 (10-3)/4=1.75 的结果长度。 |
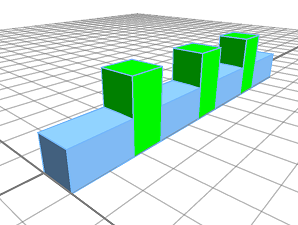 |
重复拆分 – 模式
重复操作可用于创建模式。以下示例显示几何对象可以分组到括号中并重复。
|
创建并重复一个模式。 |
 |
|
可以在其他几何图形中插入重复图案。 |
 |
重复拆分 – 平行
重复拆分可以并行执行。
|
两个重复分割(黄色和蓝色)以浮动分割(绿色)为边界。 |
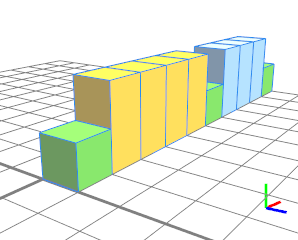 |
|
两个连续的重复分割(绿色和黄色)以绝对分割(蓝色)为界。 |
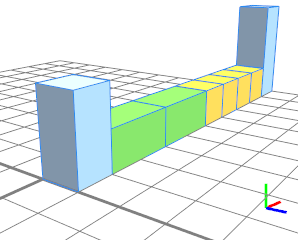 |



