分析图形 – ArcGIS CityEngine中文网

可以通过计算全局集成、局部集成和中间中心性来分析图形网络。对于每条街道，将计算这些值并将其存储为对象属性 integrationGlobal、integrationLocal 和 inbetweenCentrality。可以可视化这些值或将其用于近似街道宽度。

要打开此对话框，请选择一组图形段或图形图层，然后单击主菜单中的图形 > 分析图形。

设置


模式	可以使用以下三种模式：仅计算分析（作为对象属性）– 对于每条街道，将计算三个分析值：全局集成、局部集成和中间中心性。这些值将存储为对象属性。可视化分析（分配规则）：计算三个分析值并为街道形状分配可视化规则文件。将自动触发模型生成。可以通过选择街道形状并使用检查器来配置可视化。设置街道宽度（基于集成）– 计算三个分析值，并将局部集成映射到由“街道宽度最小值”和“街道宽度最大值”指定的范围。运行该工具后，请选择街道图层以在检查器的图层属性中查看或更改映射代码。
局部集成深度	要计算局部集成值，需要考虑 90 度转弯的数量。
街道宽度最小值	街道宽度下限；仅用于“设置街道宽度”模式。
街道宽度最大	街道宽度上限；仅用于“设置街道宽度”模式。

计算所有选定街段之间的所有最短路径。最短路径成本函数是沿路径的线段之间所有角度的总和。

对于每个街段，将对到所有其他街段的最短路径进行求和。然后，将每个总和除以段数的平方。接下来，对每个值进行取反。最后，将这些值归一化，以使每个值都位于 0 到 1 的范围内。

对于每个街段，将对比 (Depth of local integration) 90 度转弯更近的所有其他街段的最短路径进行求和。然后，将每个总和除以已访问段数的平方。接下来，对每个值进行取反。最后，将这些值归一化，以使每个值都位于 0 到 1 的范围内。

对于每个街段，将计算通过该街段的最短路径的数量。然后，将这些值归一化，以使每个值都位于 0 到 1 的范围内。

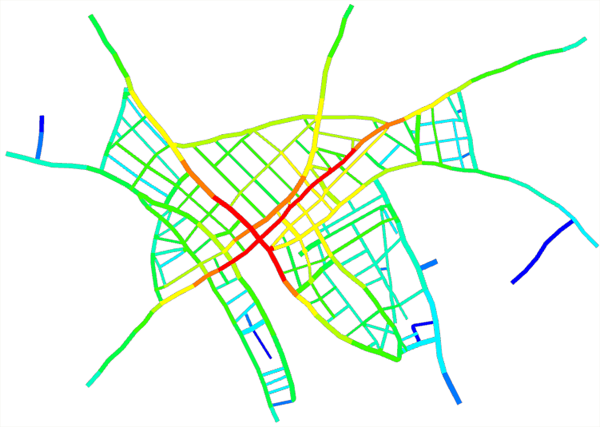
声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。